Теорема Байеса — один из столпов вероятности. Это теория, выдвинутая Томасом Байесом (1702-1761) в 18 веке. Но что именно пытается объяснить ученый? Согласно Королевской испанской академии, вероятность выражает случайным образом соотношение между количеством благоприятных случаев и количеством возможных случаев.
Да, вокруг вероятности было разработано много теорий, которые управляют нами сегодня. Когда мы идем к врачу, он прописывает нам то, что с наибольшей вероятностью подходит для нас, рекламодатели посвящают свои кампании людям, которые с наибольшей вероятностью приобретут продукт, который они хотят продвигать, мы выбираем путь, который с большей вероятностью приведет нас меньше
Один из самых известных законов вероятности — это закон полной вероятности. Для начала мы должны рассмотреть, в чем заключается закон полной вероятности. Чтобы понять это, давайте возьмем пример.
Допустим, в случайной стране 39% населения составляют женщины. Мы также знаем, что 22% женщин и 14% мужчин не имеют работы. потом, Какова вероятность (P) того, что человек, случайно выбранный из рабочей силы в этой стране, не будет работать?

Согласно теории вероятностей, данные будут выражены следующим образом:
- Вероятность того, что человек был женщина: ВЕЧЕРА)
- Вероятность того, что человек был человек: P (H)
Зная, что 39% населения составляют женщины, мы делаем вывод, что: Р (М) = 0,39.
Тогда мы понимаем, что: P (H) = 1 — 0,39 = 0,61. Также проблема серебра дает нам условные вероятности:
- Вероятность того, что человек безработный, зная, что он женщина -> P (P | M) = 0,22
- Вероятность того, что человек безработный, зная, что он мужчина —- P (P | H) = 0,14
Таким образом, используя закон полной вероятности Мы будем иметь:
P (P) = P (M) P (P | M) + P (H) P (P | H)
P (P) = 0,22 × 0,39 + 0,14 × 0,61
P (P) = 0,17
Да, вероятность того, что случайно выбранный человек является безработным, составит 0,17. Заметим, что результат находится между двумя условными вероятностями (0,22<0,17<0,14). К тому же он ближе к мужчинам, потому что в населении этой выдуманной страны они составляют большинство.
Теорема Байеса
Хорошо, теперь предположим, что взрослый человек был случайно выбран для заполнения формы, и было замечено, что у него или нее нет работы. В этом случае и с учетом предыдущего примера, какова вероятность того, что этим случайно выбранным человеком является женщина -P (M | P)-?
Для решения этой проблемы применим теорему Байеса. Таким образом, эта теорема используется для рассчитать вероятность события, заранее имея информацию об этом событии. Мы можем вычислить вероятность события A, зная также, что это событие A соответствует определенной характеристике (B), которая определяет его вероятность.
В данном случае мы говорим о вероятности того, что человек, случайно выбранный для заполнения формы, является женщиной. Но также, эта вероятность не будет независимой от того, является ли выбранный человек безработным или нет..
Формула теоремы Байеса
Как и в любой другой теореме, для вычисления вероятности нам нужна формула. В этом типе событий, формула определяется так:
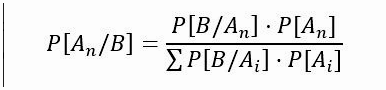
Это кажется сложным, но всему есть объяснение. Пойдем по частям. Что означает каждая буква?
- Начать, B Он событие, о котором у нас есть предварительная информация.
- Со своей стороны, письмо А (п) относится к разные условные события.
- В части числитель у нас есть условная возможность. Имеется в виду вероятность того, что что-то (событие A) произойдет, зная, что другое событие (B) также произойдет. определяется как п(К|B) и выражается как: Вероятность A при B.
- В знаменателе стоит эквивалент P (B). См. Предыдущий раздел.
Пример:
Итак, возвращаясь к предыдущему примеру, предположим, что взрослый выбран случайным образом для заполнения анкеты, и было замечено, что у него нет работы (он безработный). Какова будет вероятность того, что выбранный вами человек — женщина?
Что ж, принимая во внимание предыдущий пример, мы знаем, что 39% рабочей силы — женщины. Итак, мы знаем, что остальные — мужчины. Кроме того, мы знаем, что процент безработных женщин составляет 22%, а мужчин — 14%.
Наконец, мы также знаем, что вероятность того, что случайно выбранный человек является безработным, составляет 0,17. Итак, если мы применим формулу теоремы Байеса, мы получим, что существует Вероятность 0,5, что случайным образом выбранный из всех безработных — женщина.
P (M | P) = (P (M) * P (P | M) / P (P)) = (0,22 * 0,39) / 0,17 = 0,5
Давайте отбросим эту статью о вероятности, сославшись на одно из наиболее частых заблуждений относительно вероятности. Он колеблется между 1 и 0, никогда не покидая этих полей; где 1 — вероятность определенного события, а 0 — вероятность невозможного события..